A Minimum Variance Spectral Estimation-Based Time-Frequency Analysis for Click-Evoked Otoacoustic Emissions

 

Z. G. Zhang ^1,3 , V. W. Zhang ², S. C. Chan ³, B. McPherson², Y. Hu ¹

¹ Department of Orthopaedics and Traumatology The University of Hong Kong, Pokfulam Road, Hong Kong

² Division of Speech and Hearing Sciences The University of Hong Kong, Pokfulam Road, Hong Kong

³ Department of Electrical & Electronic Engineering, The University of Hong Kong, Pokfulam Road, Hong Kong

Dr Z. G. Zhang received his B.Sc degree from Tianjin University, China, in 2000, and graduated with an M.Phil degree in electronic engineering from the University of Science and Technology of China in 2003. He obtained his Ph.D. degree in the Department of Electrical and Electronic Engineering at the University of Hong Kong in 2008. He was a research assistant in Department of Orthopaedics and Traumatology, the University of Hong Kong, during 2008. He is currently a postdoctoral fellow in Department of Electrical and Electronic Engineering at the University of Hong Kong. His research interests are in general area of digital and biomedical signal processing.

1. Introduction

          

Traditionally, CEOAE responses are analyzed in the frequency domain via the Fourier transform. This is very useful for a primary description of CEOAE responses and is a method which aligns with clinical needs. However, CEOAEs are nonstationary signals with frequency dispersion along the time axis. Therefore, traditional spectral analysis using Fourier methods may miss some important temporal information. Recently, time-frequency analysis (TFA) of OAE has attracted increasing interest. Various TFA techniques, such as the Wigner-Ville distribution (WVD) [1], the STFT [2], the wavelet transform [3], and the matching pursuit [4], have been applied systematically to study the characteristics of different types of OAE signals. The WVD has high time-frequency resolution but it often results in severe cross-terms. The STFT originates from the Fourier transform and it faces a basic time-frequency resolution tradeoff problem, as it cannot achieve good time resolution and frequency resolution simultaneously. Wavelet transform has been proved to an effective technique for CEOAE analysis, but it has a degraded frequency resolution for high-frequency components and a degraded time resolution for low-frequency components. Matching pursuit can overcome limitations in wavelet transform by using a greedy search to expand the signal into a set of basic atoms, but its computational complexity is too heavy. In this study, a new nonparametric TFA method based on minimum variance spectral estimation (MVSE) is introduced. The MVSE is a spectral estimation algorithm which can provide higher resolution than other nonparametric spectral estimates such as the periodogram [5]. Using the same sliding window operation as in STFT, the conventional MVSE in the frequency domain can be extended to a windowed MVSE (WMVSE). Inspired by the window selection criterion of wavelet transform, we address the window selection problem of WMVSE by using a long window at low frequencies and using a short window for high frequencies. The frequency-dependent window size produces the frequency-dependent WMVSE (FDWMVSE), which can be used to analyze the time-frequency characteristics of CEOAEs.

2. Materials and Mthods

2.1. Experimental protocols

        A total of 100 neonatal CEOAE responses used in the experiments were recorded from well-baby nurseries at the Hong Kong Adventist Hospital. The average ambient room noise level with OAE equip ment in operation was less than 50 dBA. All the data fulfilled the following CEOAE criteria: stimulus stability; 75%; whole wave reproducibility ³ 70%; overall CEOAE response ³ 5 dB SPL; at least three of five test frequency bands centered at 1, 1.4, 2, 2 .8 and 4 kHz with SNR ³ 3 dB. OAE data were collected using ILO USB equipment plus V6 OAE clinical software (Otodynamics Ltd., UK). Nonlinear “ QuickScreen ” mode was used for data collection ( stimulus level of 75-80 dB peSPL ; analysis window of 12. 8ms ). Res ponse stopping criteria for CEOAE measurements required at least 70 OAE stimuli presentations, or, if no clear CEOAE response at 70 presentations, up to 260 responses were obtained.

2.2. Frequency-dependent windowed m inimum variance spectrum estimation (FDWMVSE)

          In MVSE, an adaptive filter is used to minimize the energy of other frequency components except for the desired frequency component, hence the name minimum variance. By recording the signal energy of the adaptive filter designed for different freq uencies, an energy spectrum of the input signal is obtained. Suppose the OAE signal is and the filter order is , the MVSE at a frequency of interest is calculated as

where is the by autocorrelation matrix of and .

To track the time-varying frequency contents of nonstationary CEOAEs , a windowed MVSE (WMVSE) is proposed and its idea is 1) to slide the center of a -size window to each time instant , 2) to window the input signal to yield -size data segments , 3) to calculate the autocorrelation matrix from , and 4) to obtain the WMVSE at time instant as

         The time-frequency resolution tradeoff proble m also exists in WMVSE, and the WMVSE with a fixed and for different frequency bands is not a good method . Motivated by the wavelet transfor m that uses adaptive and , a new frequency-dependent WMVSE (FDWMVSE) method is proposed (see reference [ 6 ] for full details) . The FDWMVSE uses frequency-dependent windows: shorter windows for short-duration hi gh-frequency CEOAE components to achieve good time resolution and large window sizes for long-duration low-frequency components to obtain high frequency resolution. More precisely , in the FDWMVSE method , the frequency-dependent window size is adjusted to be inverse proportional to frequency . The relation can be approximately expressed using a linear function as , where and are parameters fo r varying the window size function. In the study, with the help of a synthetic CEOAE model [3] , we estimated these parameters in a trial and error manner and determined the window size function . Then, the frequency-dependent order was chosen as .

3. Results

      One real CEOAE sample is illustrated in Fig. 1 to show the effectiveness of the proposed FDWMVSE method . For comparison , the analysis results of the wavelet transform (scalogram) method are also shown . In Fig. 1 , two components located between 3.5 kHz and 4 kHz cannot be identified in the scalogram but they are shown in the result of FDWMVSE. 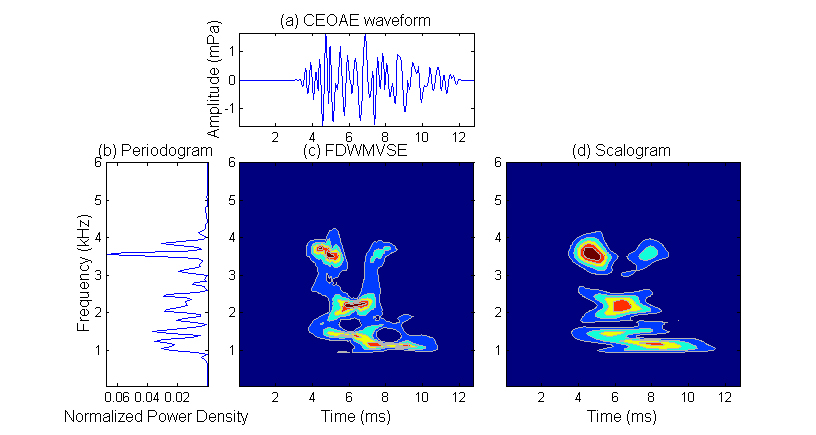Based on the periodogram and their positions, these two high-frequency components should not be spurious .

                                                                  Fig. 1 . Time-frequency representations of one real CEOAE signal using FD WMVSE and scalogram .

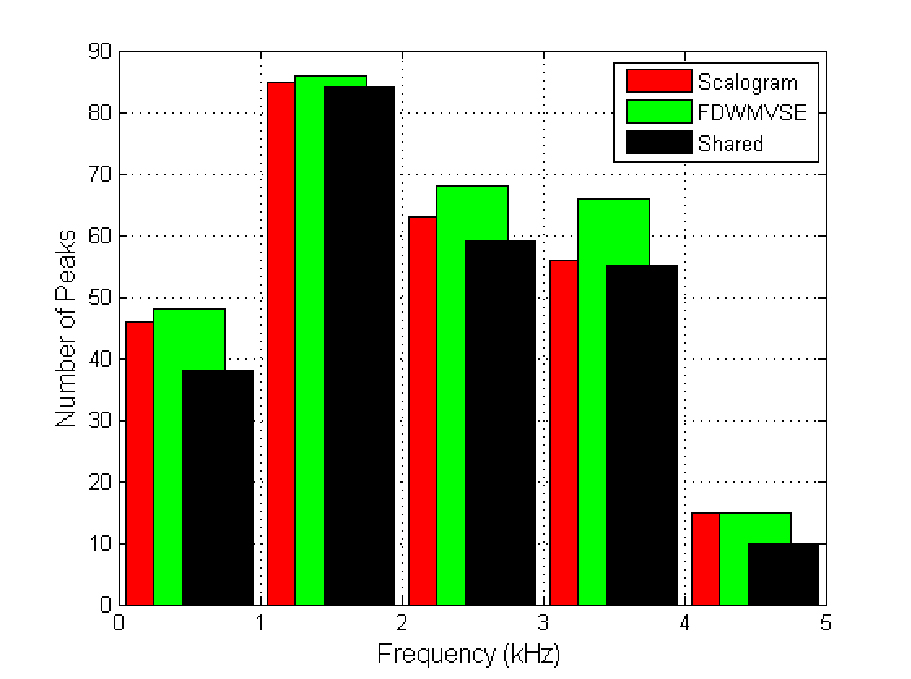
         The performance of the proposed FDWMVSE method was further assessed and compared with wavelet transform quantitatively by the parameters of peaks det ected in the time-frequency distributions. To study the characteristics of CEOAE components in different frequency bands, the whole frequency range was divided into six bands: 0 < f <= 1 kHz, 1 kHz < f <= 2 kHz, 2 kHz < f <= 3 kHz, 3 kHz < f <= 4 kHz, 4 kHz < f <= 5 kHz, and f > 5 kHz. In each frequency band, the location of its peak was detected as the time-frequency point with the maximum value of the time-frequency distribution in the f requency band . The latency and frequency of peaks can reveal meaningful information regarding CEOAE components. Further, t o compare the frequency resolution of various TFA method s , the peak width, which denotes 80% energy density of the peak power in each frequency band , was measured in both time and frequency dimensions. A narrow peak indicates a relatively high resolution, whereas a wide peak means low resolution.

          Based on the peak detection approach , the number of peaks detected in scalograms and FDWMVSE s among 100 real CEOAE signals are illustrated in Fig. 2 , where the “ shared ” peaks mean that these peaks can be detected in both scalograms and FDWMVSEs

                                                            Fig. 2 . Number of peaks detected in time- frequency representations among 100 real CEOAE signals using scalogram and FDWMVSE.

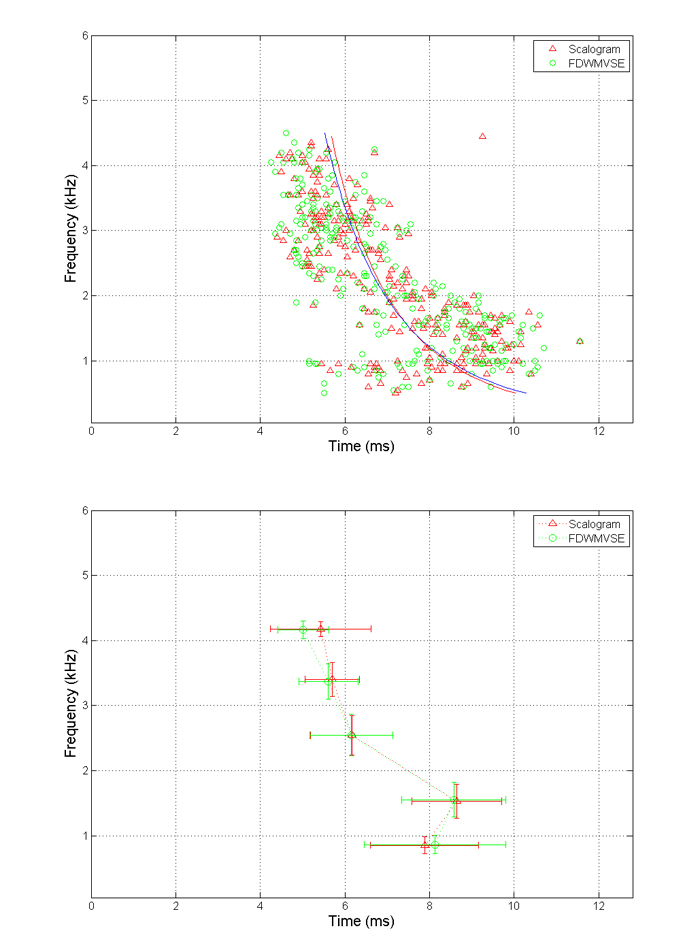
The peak distributions and the regression lines are illustrated in Fig. 3 . Using the line identification proposed in [ 7 ] , where the relation of peak latency τ (ms) and peak frequency f (kHz) was expressed as τ = κ f ^λ , we can obtain τ = 8.38 f ^-0.26 for scalogram and τ = 8.45 f ^-0.28 for FDWMVSE.

                                         Fig. 3. Distribution of peaks detected in scalogram and FDWMVSE for 100 real CEOAE signals : the upper figure shows the peak locations and the regression results and the lower figure shows
                                                   the mean and standard deviation values of peak locations at each of five frequency bands.

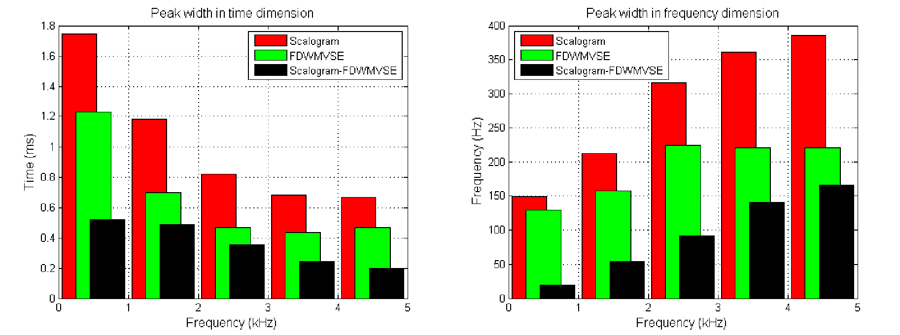
                 Last, the peak width parameters in time and frequency dimensions using scalogram and FDWMVSE are shown and compared in Fig. 4 .

                                                                                         Fig. 4 . P eak width values in time- frequency representations of 100 real CEOAE signals using scalogram and FDWMVSE.

4. Discussion

        The performances of the FDWMVSE and scalogram were evaluated and compared using the number of p eaks detected in the time-frequency distributions among all of the 100 real CEOAE data. It can be seen from Fig. 2 that, t here were most peaks in frequency band 1-2 kHz for the two methods , and FDWMVSE reveal ed slightly more power peaks (more CEOAE components) especially in frequency band 2 - 4 kHz . The reason may be that the FDWMVSE method has narrow peak widths in the frequency domain and hence it can distinguish adjacent CEOAE components in higher frequency bands.

        The distributions of peaks detected by FDWMVSE and by scalogram were also quite similar in the time-frequency domain , as seen from Fig. 3 . There were no significant differences ( p >0.05) for peak time and peak frequency between the two TFA methods. On the other hand, except for the peak width in t he frequency dimension at the frequency band 0 – 1 kHz, all other peak width values in time and frequency dimensions show significant differences ( p < 0.05) , with the peak width values of the FDWMVSE method being obviously smaller than those of scalogram. Fi g. 4 also shows that the differences of peak width in time dimension between the two methods decrease with frequency, while the differences in peak width in the frequency dimension increase with frequency. T he current results imply that the proposed FDWMVS E method has good time-frequency resolution, and this method is expected to have potential applications in CEOAE studies.

5. Conclusions

         The proposed FDWMVSE method is a good time-frequency analysis method for CEOAE because it employs frequency-dependent win dow sizes to better match the time-frequency characteristics of CEOAEs. By quantitative analysis and comparison, we can tell that the proposed FDWMVSE method has a similar performance to the classical wavelet transform in identification of peak locations at each frequency band. In higher frequency bands, FDWMVSE was able to identify more peaks due to its high frequency resolution. The FDWMVSE method can also offer smaller and narrower peak scopes than the wavelet transform.

 Acknowledgement

      This study was partially supported by the University Grants Council, Hong Kong, GRF Grant HKU7434/04M.

6. References

[1] Cheng, J., 1995. Time-frequency analysis of transient evoked otoacoustic emissions via smoothed pseudo Wigner distribution. Scand . Audiol. 24(2) , 91-96 .

[2] Hatzopoulos , S., Cheng , J. , Grzanka , A. , Martini , A., 2000. Time-frequency analyses of TEOAE recordings from normal and SNHL patients. Audiology 39(1) , 1-12.

[3] Tognola, G., Grandori, F., Ravazzani , P., 1998. Wavelet analysis of click-evoked otoacoustic emission. I EEE Trans . Biomed . Eng . 45 (6) , 686 - 697 .

[4] Jedrzejczak, W. W. , Blinowska, K. J. , Konopka, W. , 2005. Time-frequency analysis of transiently evoked otoacoustic emissions of subjects exposed to noise. Hear . Res . 205(1-2) , 249-255 .

[5] Kay, S. M. , 1987. Modern Spectral Estimation: Theory and Application . Prentice-Hall , Englewood Cliffs, NJ.

[6] Z hang , Z. G., Zhang, V. W., Chan, S. C., McPherson, B., Hu, Y., 2008. Time- frequency analysis of click-evoked otoacoustic emissions by means of a minimum variance spectral estimation-based method . Hear . Res . 2 43 (1-2) , 18-27 .

[ 7 ] Sisto, R., Morleti, A., 2002. On the frequency dependence of the otoacoustic emission latency in hypoac oustic and normal ears . J. Acoust. Soc. Am. 111(1) , 297 - 308.